高光譜成像儀在光譜數(shù)據(jù)的采集過程中,可以獲取到數(shù)量龐大的光譜數(shù)據(jù)。但這些數(shù)據(jù)中會存在大量的干擾信息,因此就需要對光譜數(shù)據(jù)進(jìn)行預(yù)處理,以提取出相應(yīng)的特征波長,建立預(yù)測模型。本文對高光譜數(shù)據(jù)特征波長的提取方法及建模方法做了介紹。
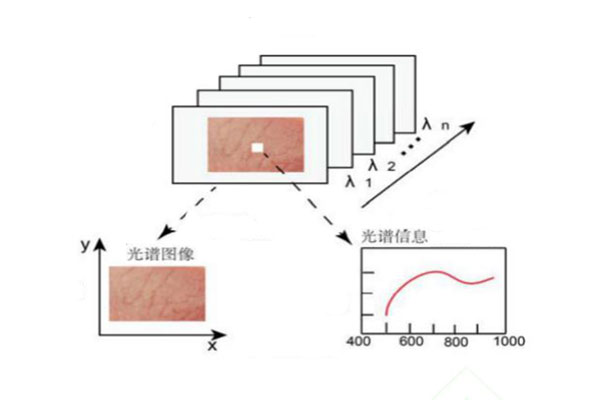
高光譜數(shù)據(jù)特征波長提取的原因:
高光譜成像儀檢測到的光譜數(shù)據(jù)由數(shù)百個波段組成,能夠獲得數(shù)百個光譜變量,光譜數(shù)據(jù)量非常大。而且光譜分析時往往需要進(jìn)行大樣本量的獲取。因此,光譜數(shù)據(jù)會顯得非常大且冗余,造成后期光譜數(shù)據(jù)處理分析時效率不高,精度不高,速度下降,提高了對數(shù)據(jù)處理的配套軟硬件要求,同時也不適于未來的工程儀器的應(yīng)用開發(fā)。
為了解決這種問題,就需要尋找有助于建模的特征變量,減少變量個數(shù),提高運算效率,優(yōu)化預(yù)測模型,提高模型預(yù)測的精度,同時也有助于開發(fā)便攜、低成本的儀器。因此需要采用光譜特征波長選擇算法來尋找有助于提高模型預(yù)測效果的特征波長變量。
高光譜數(shù)據(jù)特征波長的提取方法:
常用的特征波長提取算法有遺傳算法(GA)、競爭性自適應(yīng)重加杈算法(CARS)、無信息變量消除法(UME)、連續(xù)投影算法(SPA)、回歸系數(shù)法(RC)、Random frog等。高光譜數(shù)據(jù)分析中沒有標(biāo)準(zhǔn)的、唯一的方法選擇最佳波長。
1.Random frog方法
基于可逆跳馬爾可夫鏈蒙特卡洛算法,在模型空間中模擬一條服從穩(wěn)態(tài)分布的馬爾可夫鏈,來計算每個變量的被選概率,從而進(jìn)行變量的選擇。
2.CARS方法
模仿達(dá)爾文進(jìn)化論中的“適者生存”法則,利用指數(shù)衰減函數(shù)和自適應(yīng)重加權(quán)采樣技術(shù)去除PLSR模型中權(quán)重較小的回歸系數(shù),優(yōu)選出權(quán)重前幾的系數(shù)。
3.SPA方法
通過對光譜數(shù)據(jù)進(jìn)行一系列的投影映射構(gòu)造新的變量集,并根據(jù)多元線性回歸評價模型的預(yù)測性能,該變量集中變量的共線性最小。
4.UME方法
向PLSR模型中添加幅度較小的隨機變量矩陣,基于交叉驗證建立新的PLSR模型。將每個變量系數(shù)平均值和標(biāo)準(zhǔn)差的商作為穩(wěn)定性的值,同隨機變量矩陣得到的穩(wěn)定性的值作比較,選出被認(rèn)為和隨機變量一樣對模型建立無效的波長變量。
5.GA方法
模擬生命進(jìn)化機制,從任意一個初始群體出發(fā),產(chǎn)生一群新的更適應(yīng)環(huán)境的個體,使群體進(jìn)化到搜索區(qū)域中越來越好的區(qū)域。
6.RC方法
PLSR建模所得到的模型回歸系數(shù),挑選系數(shù)絕對值大的作為特征波長。
高光譜數(shù)據(jù)的建模方法介紹:
由于高光譜數(shù)據(jù)的復(fù)雜以及數(shù)據(jù)量很大,很難直接的對數(shù)據(jù)進(jìn)行定量定性分析,因此需要對提取得到的光譜數(shù)據(jù)采用化學(xué)計量學(xué)的方法進(jìn)行建模分析,對經(jīng)過特征波長變量提取后的光譜建立多元變量校正模型,比較不同模型的預(yù)測效果,選取最優(yōu)模型,便于以后的儀器開發(fā)應(yīng)用。目前,采用的化學(xué)計量學(xué)建模算法主要是偏最小二乘回歸法(PLSR)和最小二乘支持向量機(LS-SVM)。
1.偏最小二乘回歸法(PLSR)
PLSR是一種常見的多元統(tǒng)計方法,廣泛應(yīng)用于光譜檢測模型的建立。其原理是將因子分析和回歸分析相結(jié)合,同時將光譜數(shù)據(jù)和理化參考數(shù)據(jù)分解,采用留一法交互驗證計算預(yù)測殘差平方和,再根據(jù)潛在變量的累積貢獻(xiàn)率和預(yù)測殘差平方和,尋找最佳的潛在變量個數(shù)將光譜數(shù)據(jù)和理化參考值相關(guān)聯(lián),建立回歸模型。其優(yōu)點是較好的解決了樣本個數(shù)少于變量個數(shù)的問題。
2.最小二乘支持向量機(LS-SVM)
LS-SVM是一種改進(jìn)的支持向量機算法,能夠快速的進(jìn)行線性和非線性建棋分析,能有效解決高維數(shù)據(jù)分析問題,其算法思想是將原始樣本數(shù)據(jù)映射到高維空間里,用等式約束取代不等式約束,在高維空間里對最小化損失函數(shù)進(jìn)行求解獲得線性擬合函數(shù)。將傳統(tǒng)支持向量機的二次規(guī)劃問題,簡化成求解一個等式方程組問題,大大提高計算效率。






